워게임/CryptoHack
[CryptoHack] DIFFIE-HELLMAN (Diffie-Hellman Starter 3, 4, 5)
- -

Diffie-Hellman Starter 3

문제 및 설명
| 디피-헬만 프로토콜은 이산 로그가 주어진 그룹에 대해 "어려운" 계산으로 가정되기 때문에 사용됩니다. 프로토콜의 첫 번째 단계는 소수 p와 유한체의 생성자 g를 설정하는 것입니다. 이러한 값은 특정한 경우에 이산 로그를 효율적인 알고리즘으로 해결할 수 있는 상황을 피하기 위해 신중하게 선택되어야 합니다. 예를 들어, p = 2*q +1과 같은 안전한 소수를 일반적으로 선택합니다. 여기서 p - 1의 인수는 {2,q}로, q는 다른 큰 소수입니다. 이렇게 함으로써 디피-헬만 프로토콜을 포홀리그-헬만 알고리즘으로부터 보호할 수 있습니다. 사용자는 그런 다음 비밀 정수 a < p를 선택하고 g^a mod p를 계산합니다. 이 값은 보안이 취약한 네트워크를 통해 전송될 수 있으며, 이산 로그의 어려움이 가정되므로 비밀 정수는 계산하기 어렵게 되어야 합니다. NIST 매개 변수를 가정할 경우: g: 2 p: 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919 g^a mod p 를 한 계산한 값은 a: 972107443837033796245864316200458246846904598488981605856765890478853088246897345487328491037710219222038930943365848626194109830309179393018216763327572120124760140018038673999837643377590434413866611132403979547150659053897355593394492586978400044375465657296027592948349589216415363722668361328689588996541370097559090335137676411595949335857341797148926151694299575970292809805314431447043469447485957669949989090202320234337890323293401862304986599884732815 |
풀이
더보기

p = 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919
a = 972107443837033796245864316200458246846904598488981605856765890478853088246897345487328491037710219222038930943365848626194109830309179393018216763327572120124760140018038673999837643377590434413866611132403979547150659053897355593394492586978400044375465657296027592948349589216415363722668361328689588996541370097559090335137676411595949335857341797148926151694299575970292809805314431447043469447485957669949989090202320234337890323293401862304986599884732815
g = 2
ans=pow(g, a, p)
print(ans)
답은 해당 위 숫자이다.
Diffie-Hellman Starter 4

문제 및 설명
| 지금은 친구 앨리스로부터 받은 데이터를 사용하여 공유 비밀값을 계산하는 시간입니다. 이전과 마찬가지로 NIST 매개 변수를 사용하겠습니다: g: 2 p: 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919 앨리스로부터 다음 정수를 받았습니다: A: 70249943217595468278554541264975482909289174351516133994495821400710625291840101960595720462672604202133493023241393916394629829526272643847352371534839862030410331485087487331809285533195024369287293217083414424096866925845838641840923193480821332056735592483730921055532222505605661664236182285229504265881752580410194731633895345823963910901731715743835775619780738974844840425579683385344491015955892106904647602049559477279345982530488299847663103078045601 당신은 비밀 정수 b를 생성하고 공개 정수 B를 계산하여 앨리스에게 보냅니다. b: 12019233252903990344598522535774963020395770409445296724034378433497976840167805970589960962221948290951873387728102115996831454482299243226839490999713763440412177965861508773420532266484619126710566414914227560103715336696193210379850575047730388378348266180934946139100479831339835896583443691529372703954589071507717917136906770122077739814262298488662138085608736103418601750861698417340264213867753834679359191427098195887112064503104510489610448294420720 B: 518386956790041579928056815914221837599234551655144585133414727838977145777213383018096662516814302583841858901021822273505120728451788412967971809038854090670743265187138208169355155411883063541881209288967735684152473260687799664130956969450297407027926009182761627800181901721840557870828019840218548188487260441829333603432714023447029942863076979487889569452186257333512355724725941310490966546682790608125613166744820307691068563387354936732643569654017172 이제 당신과 앨리스는 {g, p, A, B}만을 알고 있을 때 계산하기 어려운 공유 비밀값을 계산할 수 있습니다. 당신의 공유한 비밀값은 무엇인가요? |
풀이
더보기

A = 70249943217595468278554541264975482909289174351516133994495821400710625291840101960595720462672604202133493023241393916394629829526272643847352371534839862030410331485087487331809285533195024369287293217083414424096866925845838641840923193480821332056735592483730921055532222505605661664236182285229504265881752580410194731633895345823963910901731715743835775619780738974844840425579683385344491015955892106904647602049559477279345982530488299847663103078045601
b = 12019233252903990344598522535774963020395770409445296724034378433497976840167805970589960962221948290951873387728102115996831454482299243226839490999713763440412177965861508773420532266484619126710566414914227560103715336696193210379850575047730388378348266180934946139100479831339835896583443691529372703954589071507717917136906770122077739814262298488662138085608736103418601750861698417340264213867753834679359191427098195887112064503104510489610448294420720
p = 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919
print(pow(A,b,p))
답은 위 사진의 숫자이다.
Diffie-Hellman Starter 5
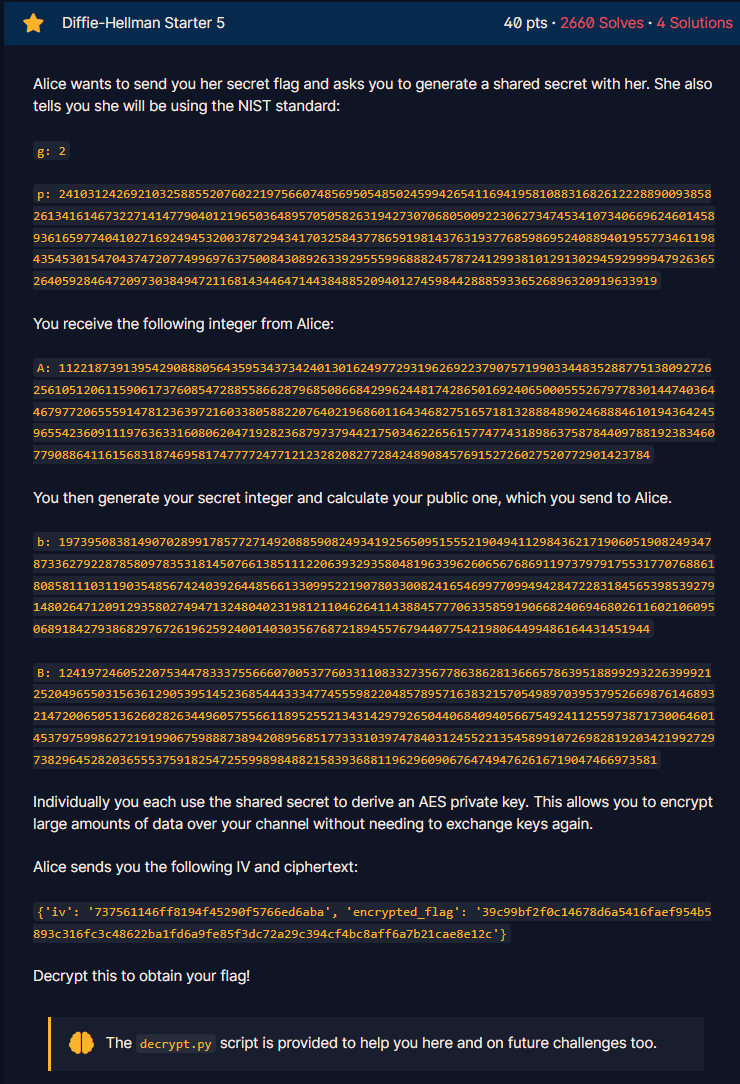
문제 및 설명
| 앨리스가 비밀 플래그를 보내고 공유 비밀값을 생성하여 함께 사용하길 원합니다. 또한, 앨리스가 NIST 표준을 사용할 것이라고 알려줍니다: g: 2 p: 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919 당신은 앨리스로부터 다음 정수를 받았습니다: A: 112218739139542908880564359534373424013016249772931962692237907571990334483528877513809272625610512061159061737608547288558662879685086684299624481742865016924065000555267977830144740364467977206555914781236397216033805882207640219686011643468275165718132888489024688846101943642459655423609111976363316080620471928236879737944217503462265615774774318986375878440978819238346077908864116156831874695817477772477121232820827728424890845769152726027520772901423784 당신은 비밀 정수를 생성하고 공개 정수 B를 계산하여 앨리스에게 보냈습니다. b: 197395083814907028991785772714920885908249341925650951555219049411298436217190605190824934787336279228785809783531814507661385111220639329358048196339626065676869119737979175531770768861808581110311903548567424039264485661330995221907803300824165469977099494284722831845653985392791480264712091293580274947132480402319812110462641143884577706335859190668240694680261160210609506891842793868297672619625924001403035676872189455767944077542198064499486164431944 B: 1241972460522075344783337556660700537760331108332735677863862813666578639518899293226399921252049655031563612905395145236854443334774555982204857895716383215705498970395379526698761468932147200650513626028263449605755661189525521343142979265044068409405667549241125597387173006460145379759986272191990675988873894208956851773331039747840312455221354589910726982819203421992729738296452820365553759182547255998984882158393688119629609067647494762616719047466973581 개별적으로 각각 공유 비밀값을 사용하여 AES 개인 키를 유도합니다. 이를 통해 키를 다시 교환하지 않고도 채널을 통해 대량의 데이터를 암호화할 수 있습니다. 앨리스는 다음 IV와 암호문을 보냈습니다: {'iv': '737561146ff8194f45290f5766ed6aba', 'encrypted_flag': '39c99bf2f0c14678d6a5416faef954b5893c316fc3c48622ba1fd6a9fe85f3dc72a29c394cf4bc8aff6a7b21cae8e12c'} 이를 복호화하여 플래그를 얻어내세요! ✍decrypt.py 스크립트는 이 문제에 도움을 주고, 향후 다른 문제에도 도와주기 위해 제공됩니다. |
풀이
더보기

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib
def is_pkcs7_padded(message):
padding = message[-message[-1]:]
return all(padding[i] == len(padding) for i in range(0, len(padding)))
def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Decrypt flag
ciphertext = bytes.fromhex(ciphertext)
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
if is_pkcs7_padded(plaintext):
return unpad(plaintext, 16).decode('ascii')
else:
return plaintext.decode('ascii')
shared_secret = ?
iv = ?
ciphertext = ?
print(decrypt_flag(shared_secret, iv, ciphertext))먼저 해당문제에서 제공한 decrypt.py이다.
{'iv': '737561146ff8194f45290f5766ed6aba', 'encrypted_flag': '39c99bf2f0c14678d6a5416faef954b5893c316fc3c48622ba1fd6a9fe85f3dc72a29c394cf4bc8aff6a7b21cae8e12c'}문제에서 이미 iv값과 encrypt_flag값은 제공해주기 때문에
공유한 비밀값인 'shared_secret'만 찾고 이를 대입을 하면된다.
4번문제에서 이를 찾는 방법이 있기에
이를 사용하면
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib
def is_pkcs7_padded(message):
padding = message[-message[-1]:]
return all(padding[i] == len(padding) for i in range(0, len(padding)))
def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
# Derive AES key from shared secret
sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]
# Decrypt flag
ciphertext = bytes.fromhex(ciphertext)
iv = bytes.fromhex(iv)
cipher = AES.new(key, AES.MODE_CBC, iv)
plaintext = cipher.decrypt(ciphertext)
if is_pkcs7_padded(plaintext):
return unpad(plaintext, 16).decode('ascii')
else:
return plaintext.decode('ascii')
A = 112218739139542908880564359534373424013016249772931962692237907571990334483528877513809272625610512061159061737608547288558662879685086684299624481742865016924065000555267977830144740364467977206555914781236397216033805882207640219686011643468275165718132888489024688846101943642459655423609111976363316080620471928236879737944217503462265615774774318986375878440978819238346077908864116156831874695817477772477121232820827728424890845769152726027520772901423784
b = 197395083814907028991785772714920885908249341925650951555219049411298436217190605190824934787336279228785809783531814507661385111220639329358048196339626065676869119737979175531770768861808581110311903548567424039264485661330995221907803300824165469977099494284722831845653985392791480264712091293580274947132480402319812110462641143884577706335859190668240694680261160210609506891842793868297672619625924001403035676872189455767944077542198064499486164431451944
p = 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919
shared_secret = pow(A,b,p)
iv = '737561146ff8194f45290f5766ed6aba'
ciphertext = '39c99bf2f0c14678d6a5416faef954b5893c316fc3c48622ba1fd6a9fe85f3dc72a29c394cf4bc8aff6a7b21cae8e12c'
print(decrypt_flag(shared_secret, iv, ciphertext))
답은 crypto{sh4r1ng_s3cret5_w1th_fr13nd5}이다.
'워게임 > CryptoHack' 카테고리의 다른 글
| [CryptoHack] HASH FUNCTIONS (Collider) (0) | 2023.07.30 |
|---|---|
| [CryptoHack] DIFFIE-HELLMAN (Script Kiddie) (0) | 2023.06.30 |
| [CryptoHack] DIFFIE-HELLMAN (Diffie-Hellman Starter 1, 2) (0) | 2023.05.31 |
| [CryptoHack] Mathmatics (Adrien's Signs) (0) | 2023.05.30 |
| [CryptoHack] MATHEMATICS (Modular Square Root) (0) | 2023.05.29 |
Contents
